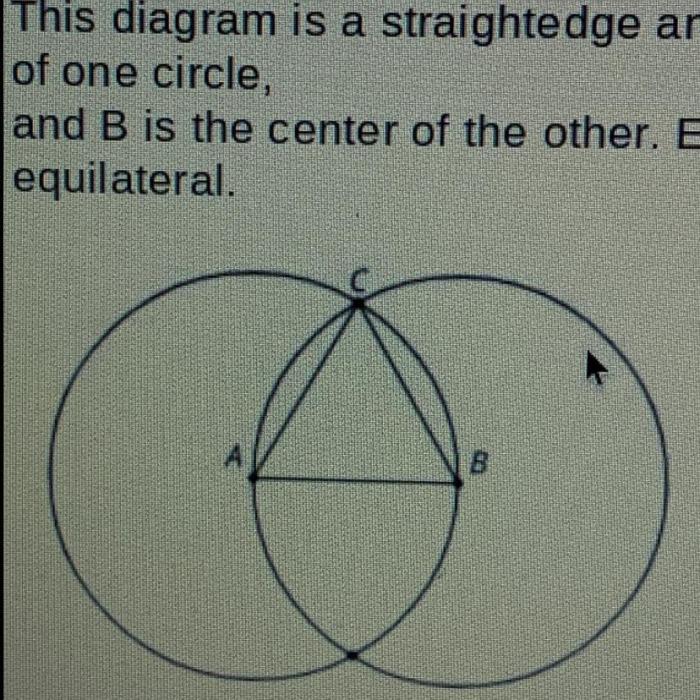
This diagram is a straightedge and compass construction, an ancient technique that has captivated mathematicians and artists for centuries. With only these simple tools, we can construct intricate geometric figures with remarkable accuracy, unlocking a world of mathematical possibilities.

Through step-by-step instructions and engaging examples, we will explore the fascinating world of compass and straightedge constructions, revealing their historical significance, geometric principles, and modern applications.

1. Definition of Compass and Straightedge Constructions: This Diagram Is A Straightedge And Compass Construction

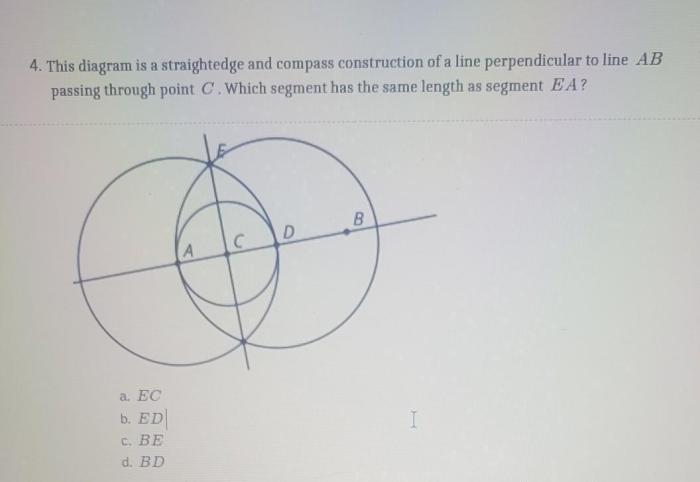
Compass and straightedge constructions are a set of geometric constructions that use only a compass and a straightedge. These tools have been used for centuries to create precise geometric figures, and they are still used today in a variety of fields, including architecture, engineering, and art.

2. Types of Compass and Straightedge Constructions

Angle Bisection

Angle bisection is the process of dividing an angle into two equal parts. To bisect an angle using a compass and straightedge, follow these steps:

1. Draw a ray from the vertex of the angle.
2. Place the compass point on the vertex of the angle and draw an arc that intersects the ray.
3. Without changing the compass setting, place the compass point on the intersection of the arc and the ray and draw another arc that intersects the first arc.
4. Draw a ray from the vertex of the angle through the intersection of the two arcs.

Line Segment Division, This diagram is a straightedge and compass construction

Line segment division is the process of dividing a line segment into two equal parts. To divide a line segment using a compass and straightedge, follow these steps:

1. Draw a circle with center at one endpoint of the line segment and radius equal to the length of the line segment.
2. Draw a circle with center at the other endpoint of the line segment and radius equal to the length of the line segment.
3. The two circles will intersect at two points. Draw a line segment connecting these two points.

Circle Construction

Circle construction is the process of creating a circle with a given radius. To construct a circle using a compass and straightedge, follow these steps:

1. Place the compass point at the center of the circle.
2. Set the compass to the desired radius.
3. Draw a circle.

3. Geometric Properties in Compass and Straightedge Constructions

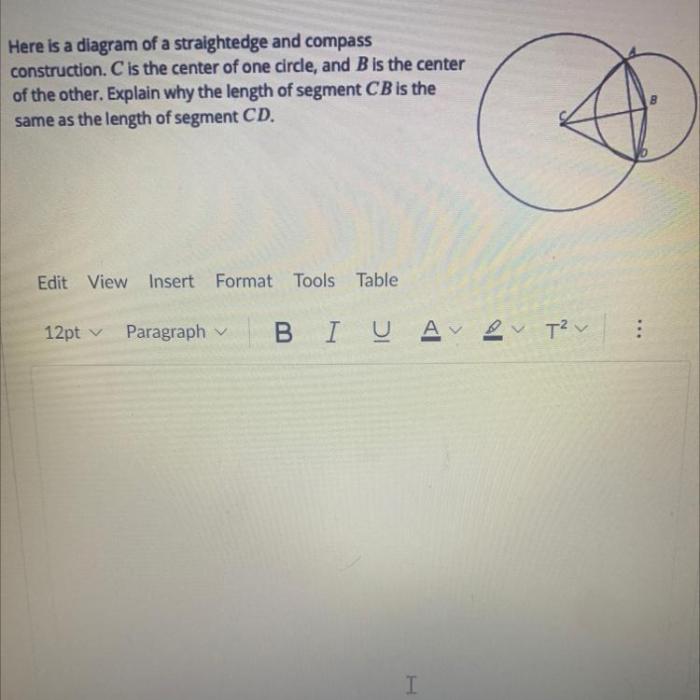
Compass and straightedge constructions preserve certain geometric properties. These properties include:

• Length: The length of a line segment is preserved.
• Angle: The measure of an angle is preserved.
• Parallelism: Two lines that are parallel remain parallel.
• Perpendicularity: Two lines that are perpendicular remain perpendicular.

4. Applications of Compass and Straightedge Constructions

Compass and straightedge constructions are used in a variety of fields, including:

• Architecture: Architects use compass and straightedge constructions to create precise plans for buildings.
• Engineering: Engineers use compass and straightedge constructions to design bridges, roads, and other structures.
• Art: Artists use compass and straightedge constructions to create geometric patterns and designs.

5. Limitations of Compass and Straightedge Constructions

There are certain geometric constructions that cannot be performed using only a compass and straightedge. These constructions include:

• Trisecting an angle: Dividing an angle into three equal parts.
• Doubling a cube: Constructing a cube with twice the volume of a given cube.

6. Interactive Demonstrations of Compass and Straightedge Constructions

There are a number of interactive demonstrations of compass and straightedge constructions available online. These demonstrations allow users to explore different constructions and see how they are performed.

7. Historical Significance of Compass and Straightedge Constructions



Compass and straightedge constructions have been used for centuries to solve geometric problems. These constructions were first developed by the ancient Greeks, and they have been used by mathematicians and scientists ever since.

8. Modern Applications of Compass and Straightedge Constructions



Compass and straightedge constructions are still used today in a variety of fields. These constructions are used to create precise geometric figures, and they are also used to solve geometric problems.

FAQ Guide

What are the limitations of compass and straightedge constructions?

Compass and straightedge constructions cannot trisect an angle or double a cube, tasks that require more advanced mathematical techniques.

How are compass and straightedge constructions used in modern applications?

These constructions find applications in computer graphics, engineering design, and architecture, enabling the creation of precise geometric shapes and patterns.